
連續模應用HD諧波減速機CSD-32-100-2A-GR,指的是壓力機在一次沖壓行程中,采用帶狀沖壓原材料,在一副模具上用幾個不同的工位同時完成多道沖壓工序的冷沖壓沖模,模具每沖壓完成一次,料帶定距移動一次,至產品完成。
連續模在沖壓過程中材料料帶始終向一個方向運動;模具內部料帶切斷后向兩個或者兩個以上方向運動的叫級進模;料帶送料在模具內部完成的叫自動連續模;在一個沖壓生產鏈上用不藝的沖壓模具用機械手或其他自動化設施,采用模具或者零件移動完成工件沖壓加工額定模具叫多工位模。
數學上的連續模:
刻畫函數的連續性的一種尺度。假設?(x)是定義在閉區間【α,b】上的連續函數,稱(圖1)為?的連續模。ω(?,δ)是在 【0,l】上有定義的函數(l=b-α),并且有如下性質:①當?δ→0時,ω(?,δ)→0;②ω(?,δ)是非負增函數;③ω(?,δ)是半可加的,也即對于(圖2)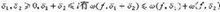 圖2;④ω(?,δ)是δ的連續函數;⑤對于自然數n, 當0≤nδ≤l時,有ω(?,nδ)≤nω(?,δ),對于非整數λ>0,當0≤λδ≤l時,有ω(?,λδ)≤(λ+1)ω(?,δ)。將ω(?,δ)看作連續函數空間上的泛函,則它具有半范數的性質,也即滿足
圖2;④ω(?,δ)是δ的連續函數;⑤對于自然數n, 當0≤nδ≤l時,有ω(?,nδ)≤nω(?,δ),對于非整數λ>0,當0≤λδ≤l時,有ω(?,λδ)≤(λ+1)ω(?,δ)。將ω(?,δ)看作連續函數空間上的泛函,則它具有半范數的性質,也即滿足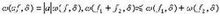 圖3(圖3)。連續模不可能太小, 對于δ→0,若(圖4),則?是個常數,從而ω(?,δ)恒等于零。
圖3(圖3)。連續模不可能太小, 對于δ→0,若(圖4),則?是個常數,從而ω(?,δ)恒等于零。
連續模的性質①②和③是本質的,倘若定義在【0,l】上的函數ω(δ)滿足這三個性質,則它必然是【α,b】上的某個連續函數的連續模。故常稱具有性質①②和③的函數為連續模函數。
如果對于任意的x,y∈【α,b】和α≥0,β≥0,α+β=1,函數g(x)滿足不等式α(g(x)+βg(y)≤g(αx+βy),則稱g在【α,b】上是凹(上凸)的。如果在【0,l】上滿足ω(0)=0的連續的增函數?ω(x)是凹(上凸)的,則它必然是連續模函數。當然,連續模未必是凹的,但是,對于每個連續模函數?ω(x)(0≤x≤l),都存在凹的連續模函數ω1(x)使得?ω(x)≤ω1(x)≤2ω(x) (0≤x≤l)。
作為連續模的直接推廣是光滑模。設r是自然數,對于【α,b】上的連續函數?(x),稱(圖5)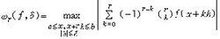 圖5為?的r階光滑模,其主要性質是,對于λ>0,有(圖6)。
圖5為?的r階光滑模,其主要性質是,對于λ>0,有(圖6)。
若?有r階連續導數,則(圖7)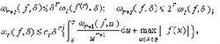 圖7式中сr與с是與?及δ無關的正數。
圖7式中сr與с是與?及δ無關的正數。